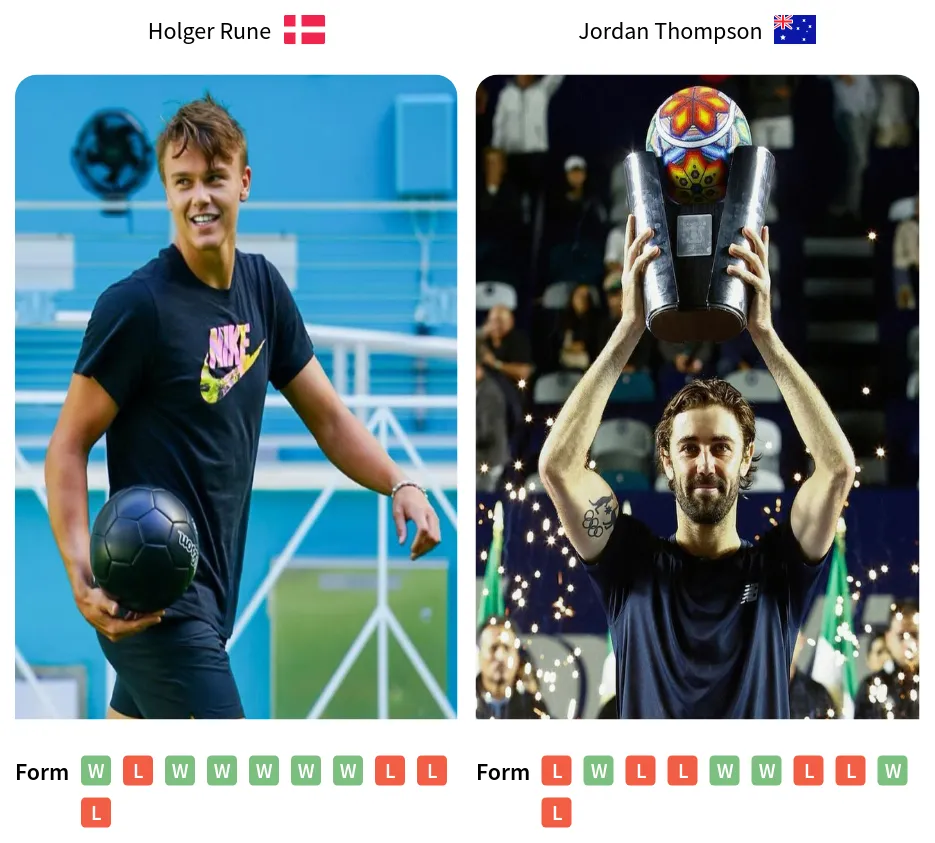
Alright, let’s dive into my recent experiment: rune vs thompson prediction. It was a bit of a wild ride, so buckle up!
First off, I wanted to see if I could build a simple predictor using runes and compare it to a more traditional Thompson Sampling approach. I started by dusting off my rusty Python skills – hadn’t touched that in a minute.
I kicked things off with the runes. I generated a sequence of random runes, and then tried to predict the next rune based on the previous ones. The approach was straightforward: I kept a count of rune transitions. So, if I saw ‘A’ followed by ‘B’ a bunch of times, my predictor would favor ‘B’ after seeing ‘A’. Super basic, I know, but hey, gotta start somewhere.
The coding part was actually pretty fun. I defined a function to generate the rune sequences, another to update the transition counts, and a third to predict the next rune. The first few runs were… well, let’s just say the accuracy was less than impressive. I’m talking like, barely above random chance. Ouch.
Next, I moved on to Thompson Sampling. This felt a bit more sophisticated. The idea here is to maintain a Beta distribution for each rune, representing our belief about its probability of success (appearing next). As we observe more runes, we update these Beta distributions. To make a prediction, we sample from each distribution and pick the rune with the highest sampled value.
Implementing Thompson Sampling took a little more effort. I had to brush up on my understanding of Beta distributions and how to sample from them. I ended up using NumPy for this, which made things a lot easier. After a bit of tweaking, I got it up and running.
Now came the interesting part: comparing the two approaches. I ran both predictors on the same rune sequences and tracked their accuracy over time. Initially, the rune-based predictor was terrible, as expected. Thompson Sampling started off a bit better, but its performance was still not great. It was pretty obvious it needed more data.
I then cranked up the length of the rune sequences. This is where things started to get interesting. The Thompson Sampling approach improved significantly with more data. It learned the underlying probabilities of the runes and started making reasonably accurate predictions. The rune-based predictor also improved, but it was still lagging behind Thompson Sampling by a significant margin.
I think the biggest takeaway for me was just how much difference the right algorithm can make, especially when dealing with limited data. The Thompson Sampling approach, with its Bayesian underpinnings, was able to learn much more effectively from the same data than my simple rune-counting method. And while this was just a toy example with runes, I can see how these principles apply to all sorts of prediction problems in the real world.

Overall, it was a pretty cool experiment. I learned a bunch, got my hands dirty with some code, and reminded myself that there’s always more to learn. Maybe next time I’ll try incorporating some neural networks into the mix. Who knows what kind of wacky predictions I’ll be making then!